Zarządzanie projektem 6 sigma. Faza Measure krok 3. Planowanie zbierania danych
Pisząc o zbieraniu danych, od razu na myśl przychodzą mi wybory prezydenckie w USA, które odbyły się w 1936r. Głównymi kandydatami byli Alf Landon oraz Franklin Delano Roosevelt. Oczywiście przeprowadzono wtedy również sondaż prezydencki przeprowadzony przez Literary Digest, na ogromnej, bo aż dwumilionowej próbie. Wyniki sondażu: Alf Landon (57%), Franklin Roosevelt (43%). Była to jedna z większych pomyłek sondażowych, bo prawdziwe wybory dały zwycięstwo Rooseveltowi, który otrzymał 61% głosów. Dodać należy, że w czasie tych wyborów dobre wskazanie zanotował dr George Gallup i to o firmie z jego nazwiskiem w nazwie często słyszymy przy okazji różnych wyborów. Gallup Organization stał się synonimem badań opinii publicznej.
Skąd taki błąd przy tak dużej próbie?
Problemem był dobór próby badawczej. Literary Digest wysłało 10 mln ankiet, z czego wróciło 2 mln (tzw. response rate). Co więcej, osoby, do których wysłano ankietę zostały znalezione w spisie abonentów telefonicznych (czyli posiadali telefon) oraz wśród posiadaczy samochodów. To oznaczało, że wybrano dość zamożną jak na tamte czasy część mieszkańców USA, wśród których przeważali sympatycy Republikanów. W badaniu pominięto natomiast ludzi biednych, którzy w większości głosowali na Roosevelta. Okazało się też, że Republikanie częściej odsyłali ankietę niż zwolennicy Demokratów (chichot losu, biorąc pod uwagę sytuację z wyborów w 2021r. Trump – Biden, gdzie to Demokraci częściej korzystali z korespondencyjnego sposobu głosowania.)
Oznacza to, że umiejętny dobór próby jest nie mniej istotny niż wielkość próbki badawczej. Można zaryzykować stwierdzenie, że nawet ważniejszy.
Jak zatem dobierać próbę w projektach Six Sigma?
Próba powinna być reprezentatywna i losowa.
Za reprezentatywną dla populacji można uznać próbę, której wszystkie cechy ściśle odzwierciedlają te same cechy populacji. Załóżmy, że pewna firma produkuje: żarówki tradycyjne (20% całości produkcji), świetlówki (30%) oraz tzw. żarówki LED (50%). Jeżeli chcielibyśmy zbadać wpływ technologii na długość działania (świecenia), to powinniśmy dobrać próbę uwzględniając powyższe proporcje.
Dodatkowo próba powinna być losowa, a to oznacza, że każdy przypadek ma takie same szanse na znalezienie się w próbce. Wiemy, że struktura próbki będzie taka, jak opisano powyżej, ale nie zostało dookreślone, która konkretna żarówka będzie podlegała badaniu.
Gdybyśmy chcieli przebadać 100 studentów, to najszybciej byśmy zrealizowali badanie idąc np. na „Wittigowo” i przepytując studentów Politechniki pędzących z akademików na zajęcia. Problem polega na tym, że nie byłaby to losowa próbka studentów. Po pierwsze, byliby to studenci z Politechniki (odcinamy inne uczelnie), po drugie mieszkający w akademikach (nie uwzględniamy wynajmujących mieszkania w mieście, ani tych z Wrocławia i okolic, którzy nie potrzebują wynajmować stancji). Po trzecie, stojąc o określonej godzinie, np. rano, nie dotrzemy do osób, które rozpoczynają zajęcia później i o tej godzinie jeszcze śpią.
Jak widać, dobór próby nie jest tak prosty jak się wydaje, a im więcej istotnych z punktu widzenia projektu optymalizacyjnego czynników uwzględnimy, tym wnioski będą bardziej miarodajne. W przypadku żarówek, warto np. pobierać próby w różnych dniach oraz w różnych godzinach na przestrzeni np. 1 miesiąca. Jeżeli praca jest zmianowa, to warto to uwzględnić, tak aby wszystkie zmiany miały swoje odzwierciedlenie w próbce. Jeżeli produkcja jest podzielona na lokalizacje (np. dwa zakłady z identycznymi liniami produkcyjnymi w różnym miastach), różne linie produkcyjne (np. różne maszyny, różny wiek maszyn, różne zużycie), to również ten aspekt powinien zostać uwzględniony. Być może proces produkcji da się podzielić na etapy. Jeżeli tak, to weźmy to pod uwagę.
To o czym napisałem powyżej jest poniekąd odstępstwem od czystego doboru losowego, gdzie każda żarówka powinna zostać ponumerowana, a następnie maszyna losująca wybierałaby konkretny numer (podobnie jak w LOTTO). Opisany powyżej dobór warstwowy (stratyfikacja) zapewnia jednak odpowiednią reprezentację zmiennych stratyfikacyjnych, a próbka tak dobrana będzie nam służyła w dalszej części projektu do analizy hipotez i ustalaniu przyczyn źródłowych.
Przez wielu dobranie próby metodą prostego doboru losowego jest taktowane niemal jak świętość, ale biorąc pod uwagę cel projektu Sigma, a także koszty ponoszone na próbkowanie, należy się starać zrobić to w sposób jak najbardziej użyteczny z punktu widzenia projektu.
Kolejnym ważnym pytaniem, które każdy badacz sobie zadaje przystępując do zbierania danych, jest pytanie o wielkość próby, tak aby szacowanie dokonane na jej podstawie miało jak największą dokładność.
Projekty, w których wykorzystuje się metodykę Sigmy, należą do grupy nieoczywistych, a co za tym idzie sporo danych należy samodzielnie wypracować przeprowadzając rozmaite eksperymenty, robiąc wdrożenia pilotażowe i weryfikując uzyskane z nich dane. Wyobraź sobie, że pracujesz w przemyśle chemicznym i masz projekt polegający na usprawnieniu procesu produkcyjnego w taki sposób, aby średnia wartość substancji X wydzielającej się w pewnym doświadczeniu uległa zwiększeniu (wzrost wydajności). Na początek poproszono Cię o oszacowanie średniej masy tej substancji, która wydziela się w obecnym procesie. Ile próbek musisz zbadać, aby z 95% pewnością ustalić średnią masę tej substancji w dokładnością +/- 0,01 grama?
Na początku nie wiadomo za dużo, więc przeprowadzacie w zespole projektowym kilka doświadczeń, aby dowiedzieć się w jakim zakresie wartości się poruszacie. 5 niezależnych doświadczeń dało następujące wyniki (w gramach):
| Nr | Wynik |
| 1 | 2,10 |
| 2 | 2,12 |
| 3 | 2,12 |
| 4 | 2,16 |
| 5 | 2,10 |
Mając te dane można wyliczyć średnią i wariancję. Korzystając np. z formuł statystycznych Excela (średnia i wariancja) wygląda to następująco:
| Średnia: | 2,12 | =ŚREDNIA(B2:B6) |
| Wariancja: | 0,0006 | =WARIANCJA.PRÓBKI(B2:B6) |
Gdyby to było wszystko, świat byłby za prosty. Brakuje jeszcze wartość odczytanej z tablic statystycznych. Próbka jest mała (5 sztuk), zatem najlepiej skorzystać z rozkładu t-Studenta (bardzo podobny do rozkładu normalnego, a do tego dobrze się sprawdza przy małych próbkach). Gdyby to były zajęcia ze statystyki, teraz wyjęlibyśmy tablice w poszukiwaniu odpowiednich wartości, ale nie każdy jest fanem statystyki, a poza tym mamy XXI wiek.
Zgodnie z założeniami, chcieliśmy mieć 95% pewności, że średnia masa wyliczona z próbki będzie odpowiadała masie substancji wytwarzanej w skali przemysłowej. Co za tym idzie dopuszczamy 5% ryzyko błędu (100% – 95% = 5%). Jest to tzw. poziom istotności zapisywany grecką litera alfa (α).
Excel w formule (ROZKŁ.T.ODWR.DS) zwracającej odwrotność rozkładu t-Studenta, upomni się jeszcze o liczbę stopni swobody, wyliczaną jako liczba eksperymentów minus jeden (5 – 1 = 4). Podstawiając dane do formuły Excela uzyskujemy wynik 2,776.
| Wartość statystyki T | 2,776 | =ROZKŁ.T.ODWR.DS(0,05;4) |
Teraz w prosty sposób można wyliczyć minimalną wielkość próbki korzystając ze wzoru:
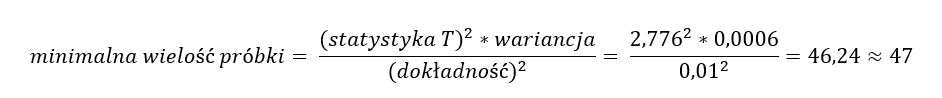
Po przeprowadzonych wyliczeniach można powiedzieć, że oprócz 5 próbek które już mamy, należy jeszcze dokonać 42 pomiarów. Dopiero mając próbkę licząca minimum 47 sztuk, będziemy mogli z 95% pewnością powiedzieć, że średnia masa uzyskiwana w tym procesie wynosi (….tu wstawiamy wyliczenie średniej z min. 47 pomiarów….), z dopuszczalnym maksymalnym błędem pomiaru sięgającym 0,01 grama.
W projektach Six Sigma często pracuje się na danych jakościowych typu: dobry/zły, poprawny/ wybrakowany. Jak sobie poradzić z takim przypadkami?
Teraz przykład przeniesie Cię do hurtowni, która specjalizuje się przechowywaniu i dystrybucji konserw. Niestety dział jakości stwierdził nieprawidłowości w przechowaniu pewnej partii towaru. Szacuje się że ok. 10% partii mogło się zepsuć (historycznie był kiedyś podobny przypadek, stąd dział jakości zaczerpnął dane, ale gdyby to był pierwszy raz, trzeba by było otworzyć jakąś część i to zweryfikować). Naszym zadaniem jest oszacowanie ilości puszek, które należy sprawdzić, aby na 90% być pewnym, jaki jest faktyczny procent zepsutych konserw, z dokładnością do +/-5%.
W przypadku tego typu problemów korzystamy ze wzoru, który opiera się na frakcjach oraz bazuje na najbardziej rozpowszechnionym rozkładzie, czyli rozkładzie normalnym.
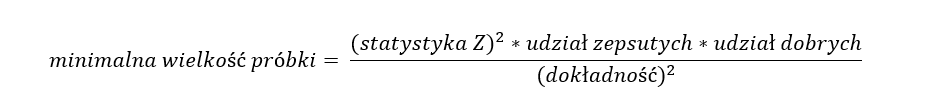
Mamy zatem takie dane:
- udział puszek zepsutych = 10% = 0,1
- udział puszek dobrych = 100% – 10% = 90% = 0,9
- dokładność pomiaru = 5% = 0,05
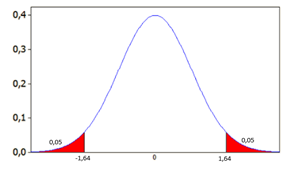
Zostaje najtrudniejsze, czyli wyliczenie statystyki Z. Technicznie rzecz ujmując chcemy sprawdzić, dla jakiego parametru Z powierzchnia pod krzywą rozkładu normalnego wyniesie 90% (wymagany przez dział jakości poziom pewności odnośnie procentu zepsutych puszek. To oznacza, że poziom istotności (α) wynosi 10%, przy czym, z uwagi na to, że rozkład ten jest dwustronny, te 10% rozkładają się równo po obu stronach krzywej (2 x po 5%). W Excelu wybieramy funkcję ROZKŁ.NORMALNY.S.ODWR(). Funkcja ma tylko jeden argument (prawdopodobieństwo). Prawdopodobieństwo wpisywane do funkcji wyniesie zatem (1 – α/2 = 1 – 0,05 = 0,95), a wynik funkcji to 1,64.
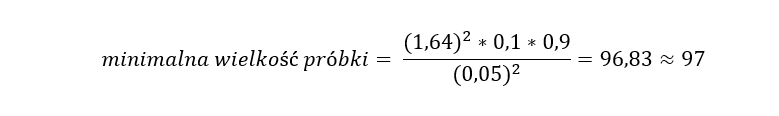
Chcąc zatem poznać procent zepsutych konserw należy z danej partii losowo wybrać minimum 97 puszek.
Uwaga: w Sigmie najczęściej używa się poziomu istotności (α) = 0,05, natomiast poniżej pokazano wartości Statystyki Z dla α od 0,01 do 0,1. Może się przydadzą w Twoim projekcie.
| poziom istotności α | Z |
| 0,01 | 2,576 |
| 0,02 | 2,326 |
| 0,03 | 2,170 |
| 0,04 | 2,054 |
| 0,05 | 1,960 |
| 0,06 | 1,881 |
| 0,07 | 1,812 |
| 0,08 | 1,751 |
| 0,09 | 1,695 |
| 0,1 | 1,645 |
O odpowiednią wielkość próbki należy też zadbać przymierzając się do analizy hipotez badawczych. Testy są różne i różna jest ich moc statystyczna, ale o tym kilka słów w jednym z kolejnych artykułów.